¶ Модели обработки последовательностей
Обработка последовательности - это преобразование некоторой последовательности в последовательность . Далее будем рассматривать общий случай, при котором и могут быть непрерывными (функции и соответственно)
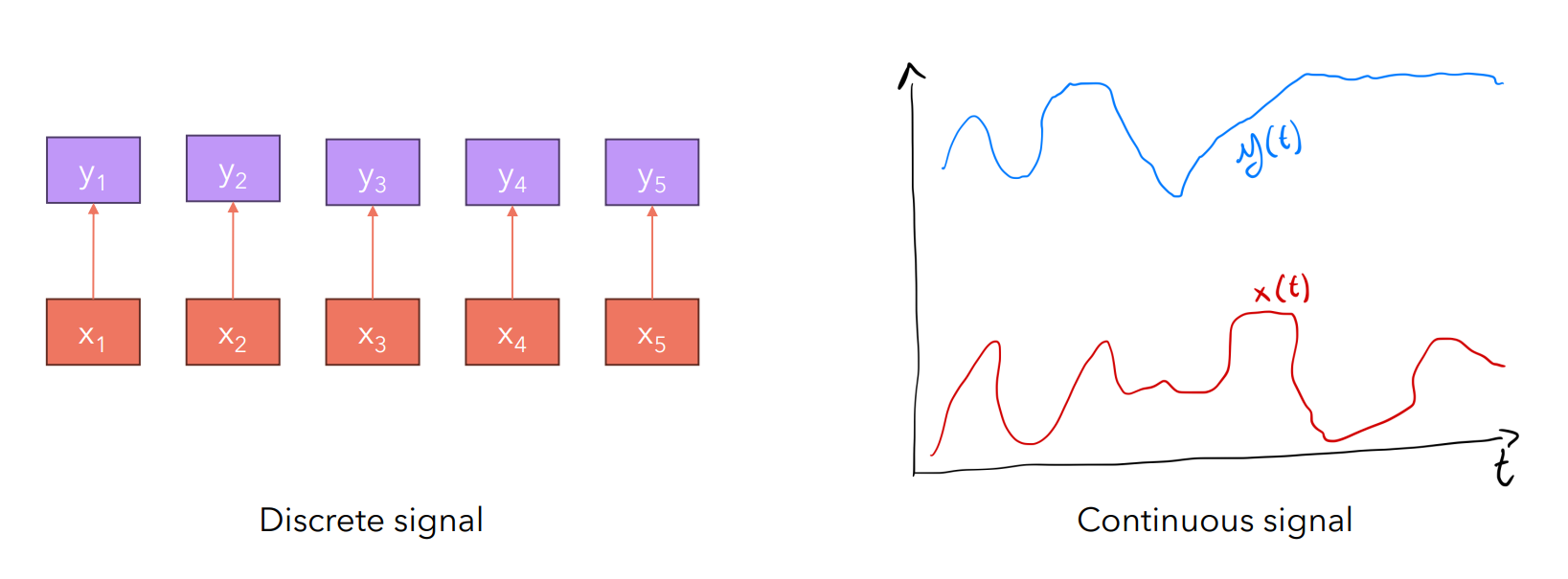
Говоря о языковом моделировании мы говорим о дискретных последовательностях (сигналах), поскольку считаем, что последовательности состоят из конечного количества токенов, которые могут быть пронумерованы.
Еще раз посмотрим на модели для обработки последовательностей, которые знаем:
¶ Рекуррентные нейронные сети
- бесконечный размер контекста, при этом наблюдается эффект забывания
- есть проблемы с угасающими и взрывающимися градиентами
- асимптотическая сложность алгоритма обучения , при этом нет возможности распараллелить
- асимптотическая сложность алгоритма инференса
¶ Трансформеры
- конечный размер контекста
- асимптотическая сложность алгоритма обучения , при этом параллелится (Multi Head Attention)
- асимптотическая сложность алгоритма инференса .
¶ Идеальный вариант:
- асимптотика и возможность распараллеливания при обучении
- асимптотика при инференсе для каждого токена
¶ Модели пространства состояний
¶ Определение
Традиционным инструментом моделирования состояния системы в произвольный момент времени являются дифференциальные уравнения. Решение уравнения позволяет найти функцию состояния . При этом будем считать, что значение задано.
Линейной моделью непрерывного пространства состояний (Space State Model) называют следующую пару уравнений:
где , , и - матрицы параметров, которые не зависят от .
Для того, чтобы вычислять значения выходного сигнала на основе входного сигнала необходимо предварительно определить . При этом мы знаем, что аналитическое решение дифференциальных уравнений для реальных систем зачастую затруднительно, если вообще возможно. При этом на практике (в частности в NLP) мы работаем с дискретными сигналами. Рассмотрим дискретизацию модели пространства состояний.
¶ Дискретизация модели
Найти приближенное решение дифференциального уравнения означает найти последовательность , , , ... Таким образом, вместо поиска мы хотим найти = , где - это наш размер шага. В примере выше .
Рекуррентная формула для дискретизации выводится следующим образом (метод Эйлера):
считая наш размер шага достаточно малым получаем:
умножая левую и правую части на получаем рекуррентную формулу:
Таким образом имеем:
где - единичная матрица.
Линейная модель дискретного пространства состояний выглядит следующим образом:
где и - дискретизированные матрицы.
При этом:
- для дискретизации матриц могут использоваться различные подходы; сегодня часто применяется экстраполятор нулевого порядка (Zero-Order Hold); в том числе он используется и в статье по архитектуре Mamba; формулы для вычисления дискретизированных матриц выглядят следующим образом:
- на практике матрица D в модели пространства состояний не используется, поскольку процесс получения на основе характеризуется матрицами , и ; в этом случае матрица D служит для реализации сквозной связи (skip connection) и в данной модели является избыточной (ранее мы использовали сквозные связи для преодоления проблемы затухающих градиентов);
- является одним из параметров модели наравне с весами (элементами рассмотренных матриц); таким образом при выполнении алгоритма обратного распространения ошибки мы сможем настраивать дискретизацию модели.
Предполагается, что размерности элементов входной и выходной последовательностей совпадают
В случае, когда размерность элементов входной последовательности больше 1, рассматривается как вектор этой размерности
¶ Seq2Seq
Дискретная модель пространства состояний является обобщением рекуррентных нейронных сетей. Положим (по аналогии - нулевой вектор). Тогда:
Далее:
Как обозначалось ранее, такие рекуррентные вычисления отлично подходят для инференса, поскольку в языковых моделях мы всегда генерируем по одному токену за раз, учитывая промпт и ранее сгенерированные токены. Но для обучения рекуррентные вычисления не подходят. Поэтому попробуем использовать то, о чем ранее не говорили в контексте обработки языка - операция свертки.
Обобщим вычисления, приведенные выше:
Получаем формулу:
Если рекуррентная формула построена на основе ассоциативной операции (в нашем случае это сумма), значит она может быть распараллелена с помощью следующей технологии:
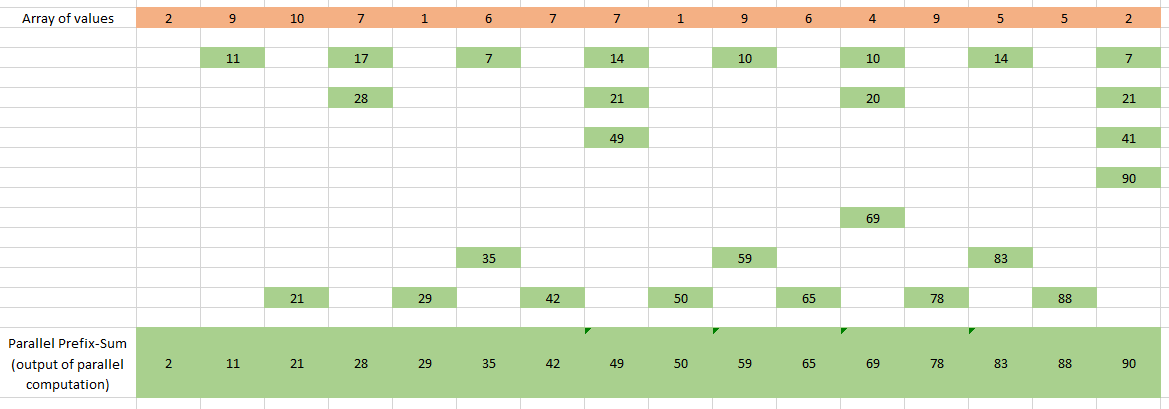
На рисунке выше у нас есть несколько потоков, каждый из которых реализует бинарную операцию (сумму).
Теорема:
Выход может быть вычислен на основе по рекуррентной формуле за счет применения к последовательности свертки с ядром следующего вида:
где - длина последовательности, которую мы хотим получить (выходной последовательности). Ядро свертки передставляет из себя последовательность матриц.
Доказательство:
Сделаем пару замечаний:
- свертку будем производить перемещением ядра слева-направо, при этом padding последовательности будем выполнять с левой стороны (если padding производится с правой стороны, то свертку необходимо производить справа-налево);
- на рисунках ниже элементы последовательностей нумеруются с нуля, в то время, как в формулах выше они нумеровались с 1; пожалуйста, не запутайтесь
¶ Шаг 0: инициализация ядра
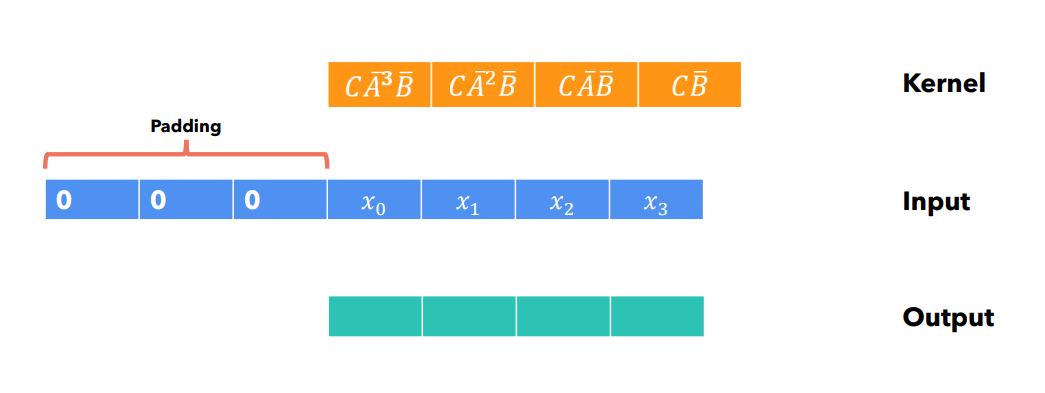
¶ Шаг 1:
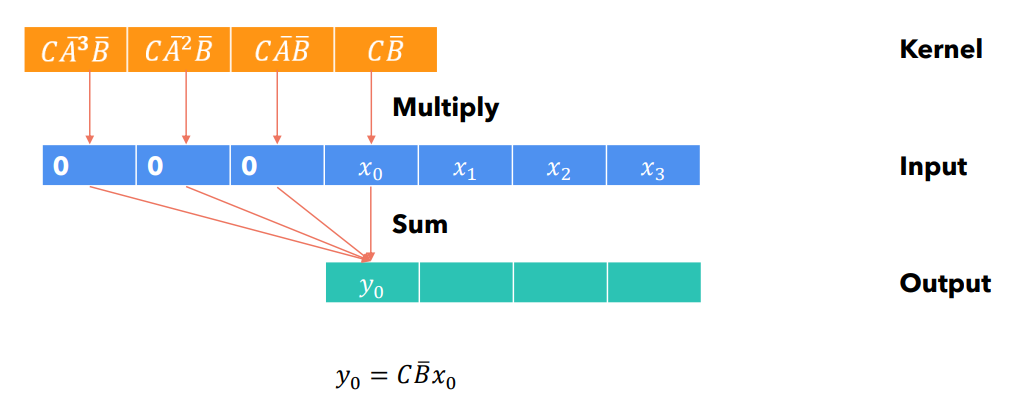
¶ Шаг 2:
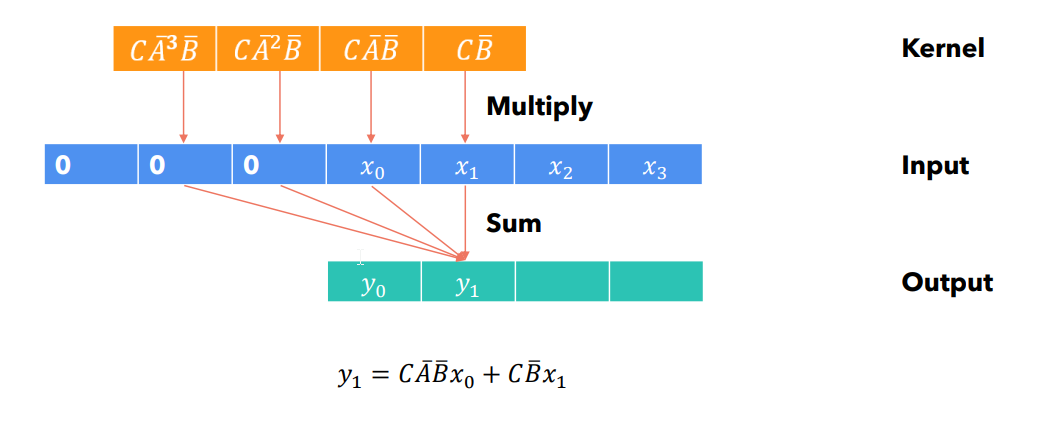
¶ Шаг 3:
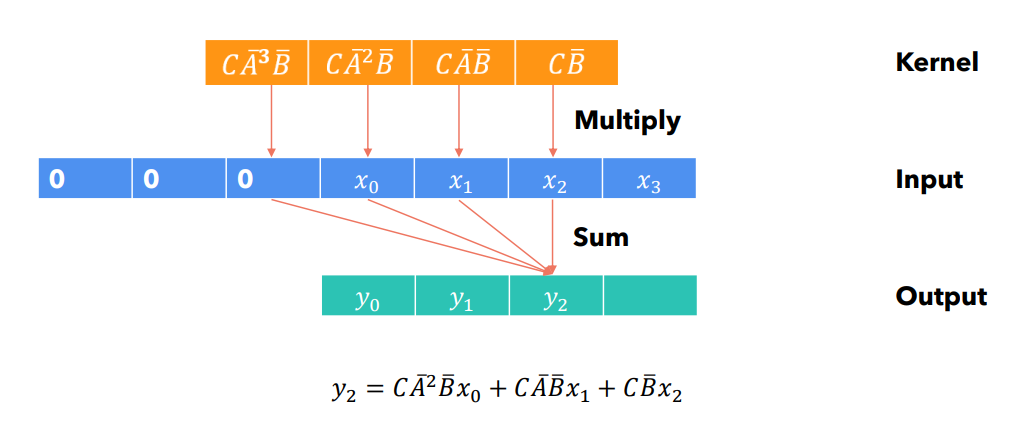
¶ Шаг 4:
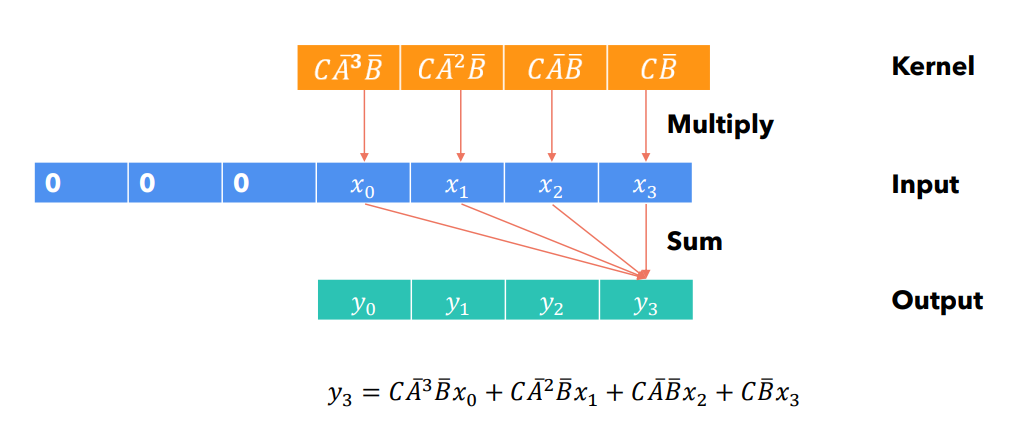
Сверточные вычисления могут быть распараллелены: не зависит от . Каждый элемент выходной последовательности определяется исключительно элементами входной последовательности и параметрами. При этом, в ходе инференса, построение ядра - затратно с точки зрения использования памяти.
Таким образом:
- мы можем использовать сверточные вычисления при обучении (есть возможность распараллелить),
- а в ходе инференса для получения элементов выходной последовательности использовать рекуррентную формулу (асимптотика при этом ).
¶ Модель структурированного пространства состояний
В целях улучшения эксплуатационных характеристик моделей необходимо обращать особое внимание на изначальную структуру матрицы , поскольку эта матрица играет ключевую роль - строит новое состояние на основе предыдущего состояния и (что важно) информации обо всех предыдущих состояниях. При этом важно, чтобы актуальное состояние в большей степени определялось последними наблюдаемыми состояниями и в меньшей степени ранними историческими состояниями.
В исследовании 2021 года предлагается инициализировать матрицу как HiPPO-матрицу:
Модели пространства состояний, в которых матрица инициализируется рассмотренным выше способом, называют моделями структурированного пространства состояний (Structured State Space Model - SSSM, иногда называют S4).
В S4 матрицы , и являются квадратными (размерность элементов входной последовательности совпадает с размерностью состояния )
¶ Архитектура Mamba
Данная архитектура описана в статье 2023 года, основана на S4 и отличается следующими возможностями:
- выборочное сканирование (Selective Scan): для фильтрации нерелевантной информации из входной последовательности;
- параллелизация рекуррентных вычислений (Parallel Scan) с применением комбинированного ядра свертки.
Архитектура Mamba по-другому называется Selective Structured State Space Model (S6).
¶ Проблема контекстной осведомленности
В виду отсутствия аналога механизма внимания модель не может концентрироваться на конкретных токенах входной последовательности.
Рассмотрим задачу выборочного копирования (выбрать из последовательности слов только существительные):
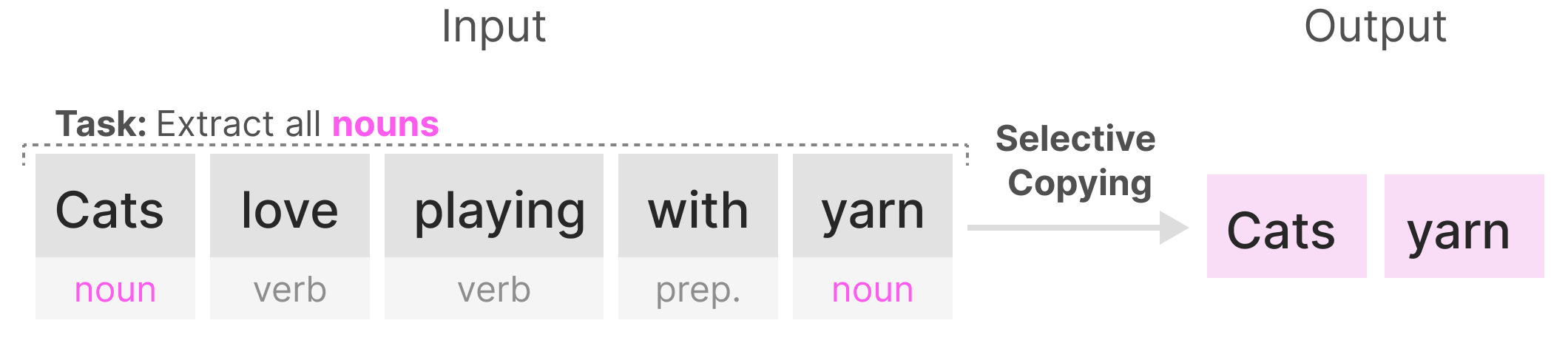
S4 плохо справится с такой задачей, поскольку матрицы , и одинаковы для каждого токена входной последовательности.
Также рассмотрим задачу вопроизведения паттернов:
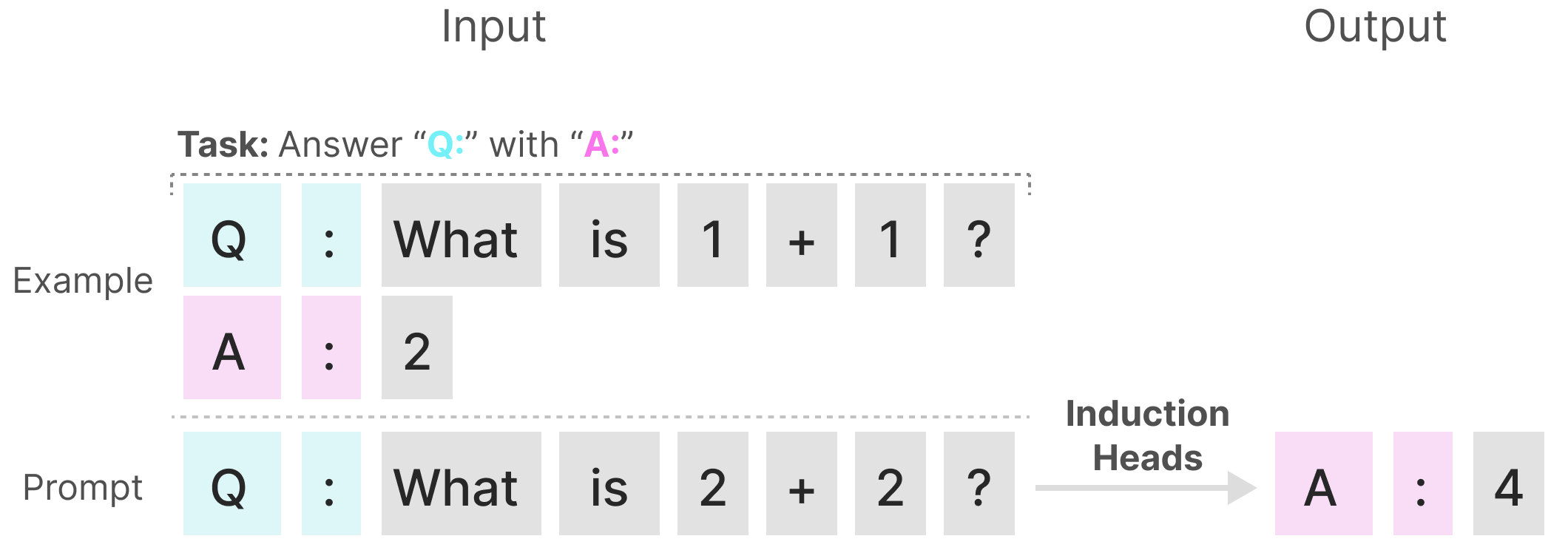
При таком одноразовом промптинге (one-shot prompting) S4 не сможет вспомнить предыдущие токены. Инвариантность модели по времени приводит к проблеме контекстной осведомленности (content-awareness).
¶ Выборочное сохранение информации
Архитектура Mamba создана, чтобы сохранить преимущества трансформеров и рекуррентных нейронных сетей:
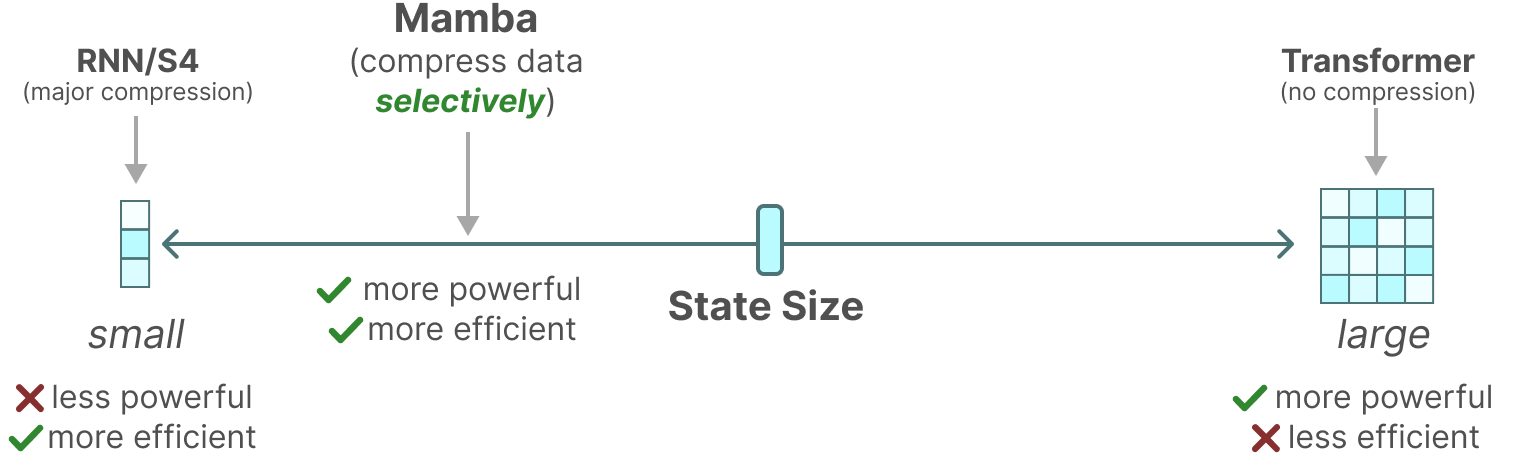
В целях решения проблемы контекстной осведомленности авторы Mamba предложили свой вариант вычисления матриц , , и шага . Модификация предполагает добавление в модель обучаемых линейных слоев:

Здесь:
- - размер батча;
- - длина входной и выходной последовательности (по аналогии с транформерами мы ее фиксируем);
- - размерность элементов входной последовательности;
- - размерность состояния;
- Linear - линейный слой (без активации);
- Broadcast - операция транслирования тензоров
- softplus - функция активации (также называемая "мягкой" ReLU); значение вычисляется по формуле .
¶ Блок Mamba
Подобно трансформерам модель Mamba представляется в виде нескольких последовательно размещенных блоков. Один блок выглядит следующим образом:
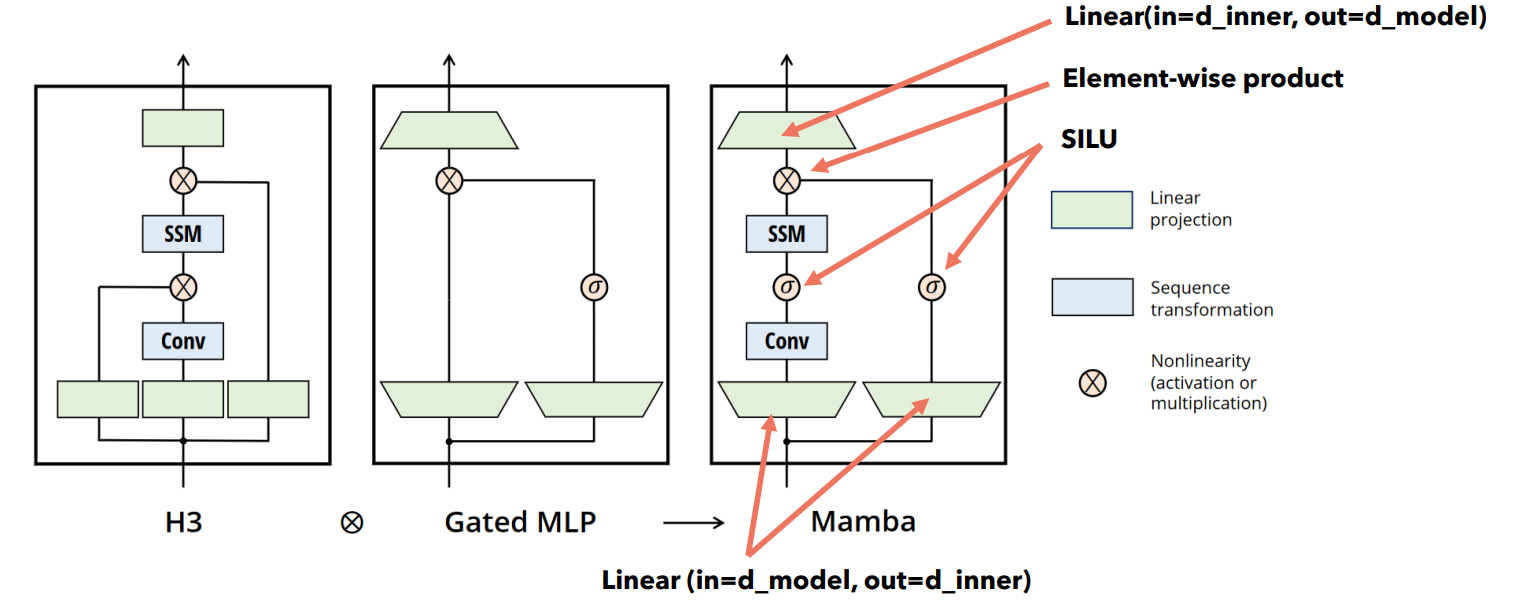
Рассматриваемая архитектура основана на архитектуре Hungry Hungry Hippo (H3) и подходе с использованием сквозной связи вместе с передаточной функцией (функцией активации).
Здесь Conv - это полноценный обучаемый сверточный Seq2Seq-слой, а SILU - функция активации , где - сигмоид.
Основные гиперпараметры модели:
- размерность внутреннего эмбеддинга (d_model, а на рисунке это d_inner!);
- размерность вектора состояния (d_state, обычно совпадает с d_model);
- размерность ядра свертки (d_conv);
- количество блоков.
В целом модель в архитектуре Mamba выглядит следующим образом:
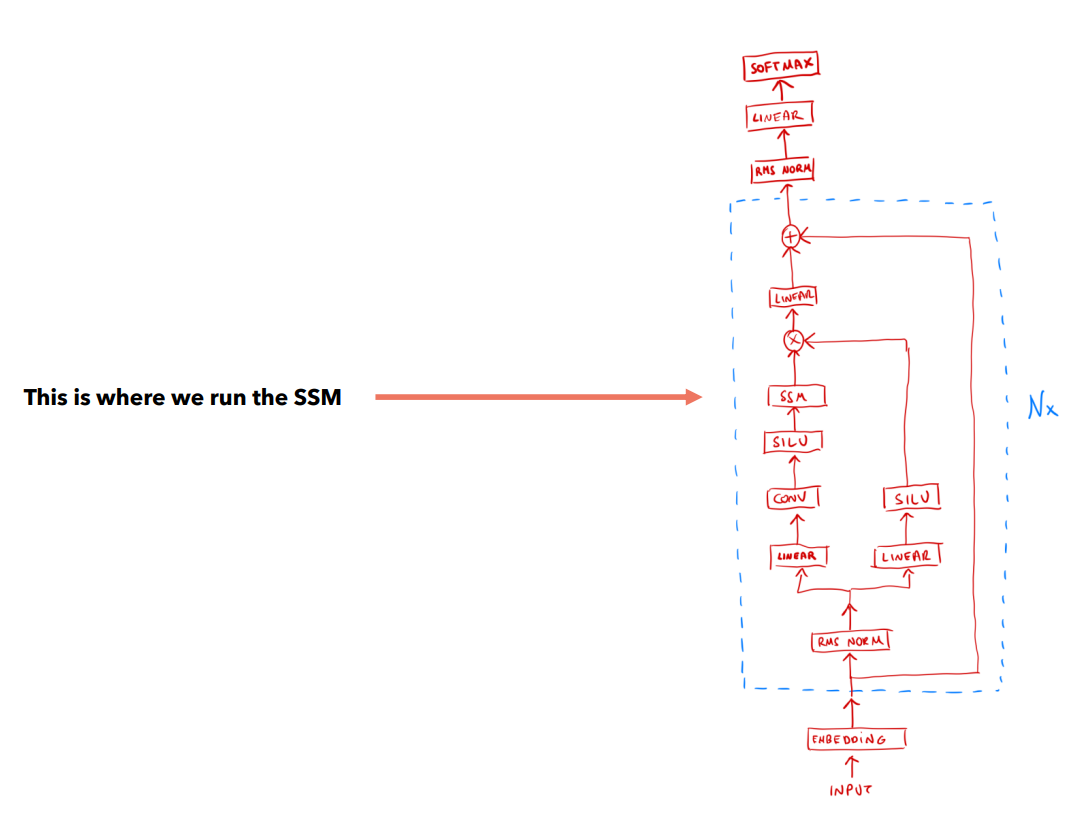
Здесь RMS Norm - это Root Mean Square Layer Normalization:
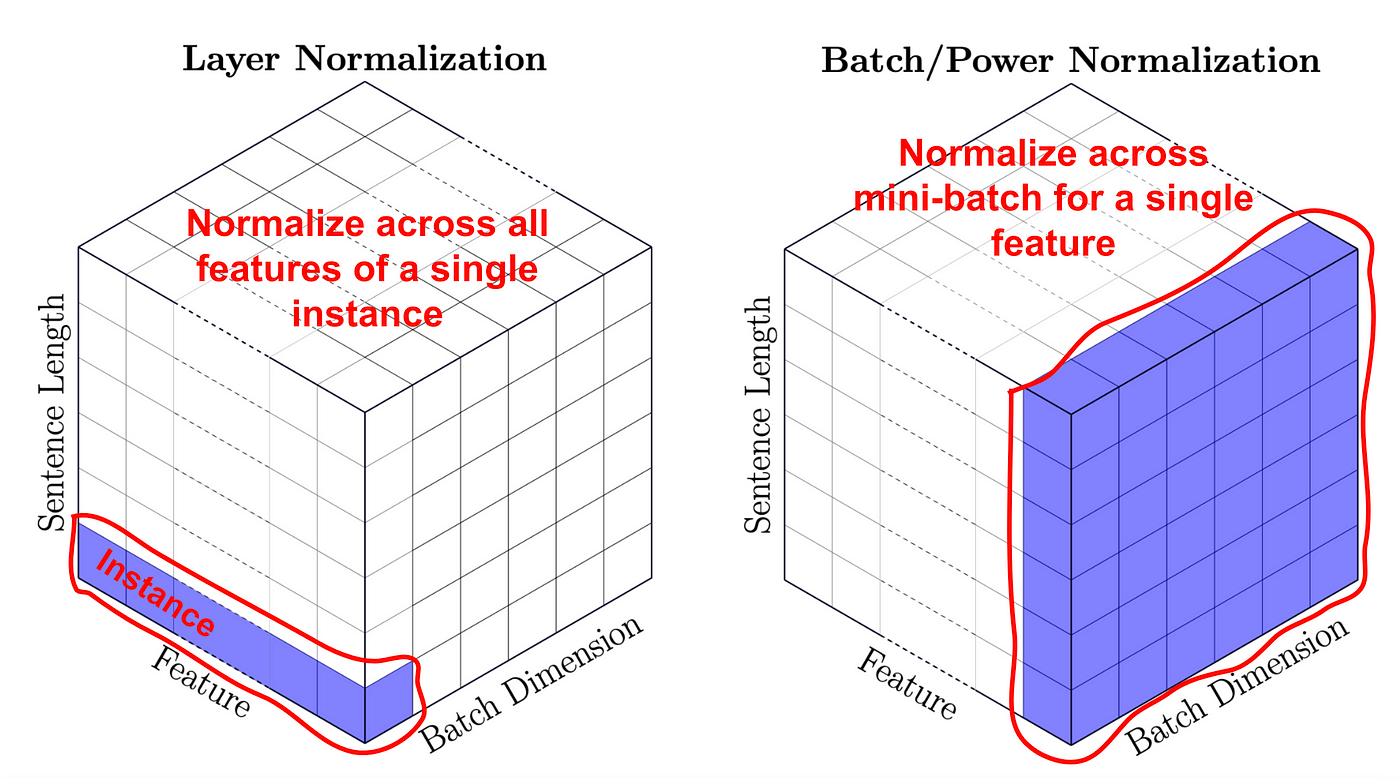
Применяется к каждому вектору входной последовательности. Следует помнить про отличие Layer Norm от Batch Norm:
¶ Выводы
Несмотря на высокие показатели эксплуатационных характеристик (метрик) качества и широкое распространение в современных LLM, архитектура Transformer не идеален. Актуальные задачи требуют увеличения контекста, а следовательно увеличения размеров входных и выходных последовательностей при инференсе. Возможность распараллеливания обучения не спасает трансформеры от замедляющегося по мере увеличения размера выходной последовательности инференса.
Современные исследования в области Seq2Seq изучают различные способы улучшения рекуррентных вычислений, интегрируя в классические схемы с состоянием аналоги механизма внимания.
Одним из последних достижений в области языкового моделирования является архитектура Mamba. Ее авторы развили идеи моделей пространства состояний, предложив решение проблемы контекстной осведомленности. Известные разработчики LLM (например Mistral AI) уже интегрируют эту архитектуру в свои решения. Исследовали продолжают работу в направлении повышения эффективности обработки тензоров на GPU.
Реализация Mamba представлена в виде репозитория и пакета mamba-ssm для PyPI.
Модель также можно попробовать на HuggingFace с помощью библиотеки transformers. Несколько любопытных ссылок: